Sections
- Sections
- Principal Component Analysis
- PCA and linear dimensionality reduction
- Nonlinear dimensionality reduction
- Kernel functions and the kernel trick
- Gaussian radial basis function (RBF) Kernel PCA
- Implementing the RBF kernel PCA step-by-step
- Examples of RBF Kernel PCA
- Appendix A: Projecting new data
- References
Principal Component Analysis
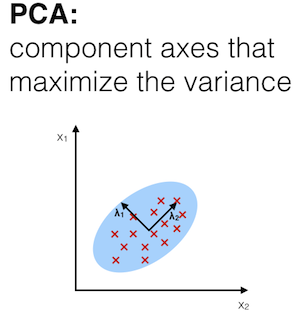
The main purpose of principal component analysis (PCA) is the analysis of data to identify patterns that represent the data “well.” The principal components can be understood as new axes of the dataset that maximize the variance along those axes (the eigenvectors of the covariance matrix). In other words, PCA aims to find the axes with maximum variances along which the data is most spread.
PCA and linear dimensionality reduction
A common application of PCA is to reduce the dimensions of the dataset with minimal loss of information. Here, the entire dataset (d dimensions) is projected onto a new subspace (k dimensions where k < d). This method of projection is useful in order to reduce the computational costs and the error of parameter estimation (“curse of dimensionality”).
The standard PCA approach can be summarized in six simple steps:
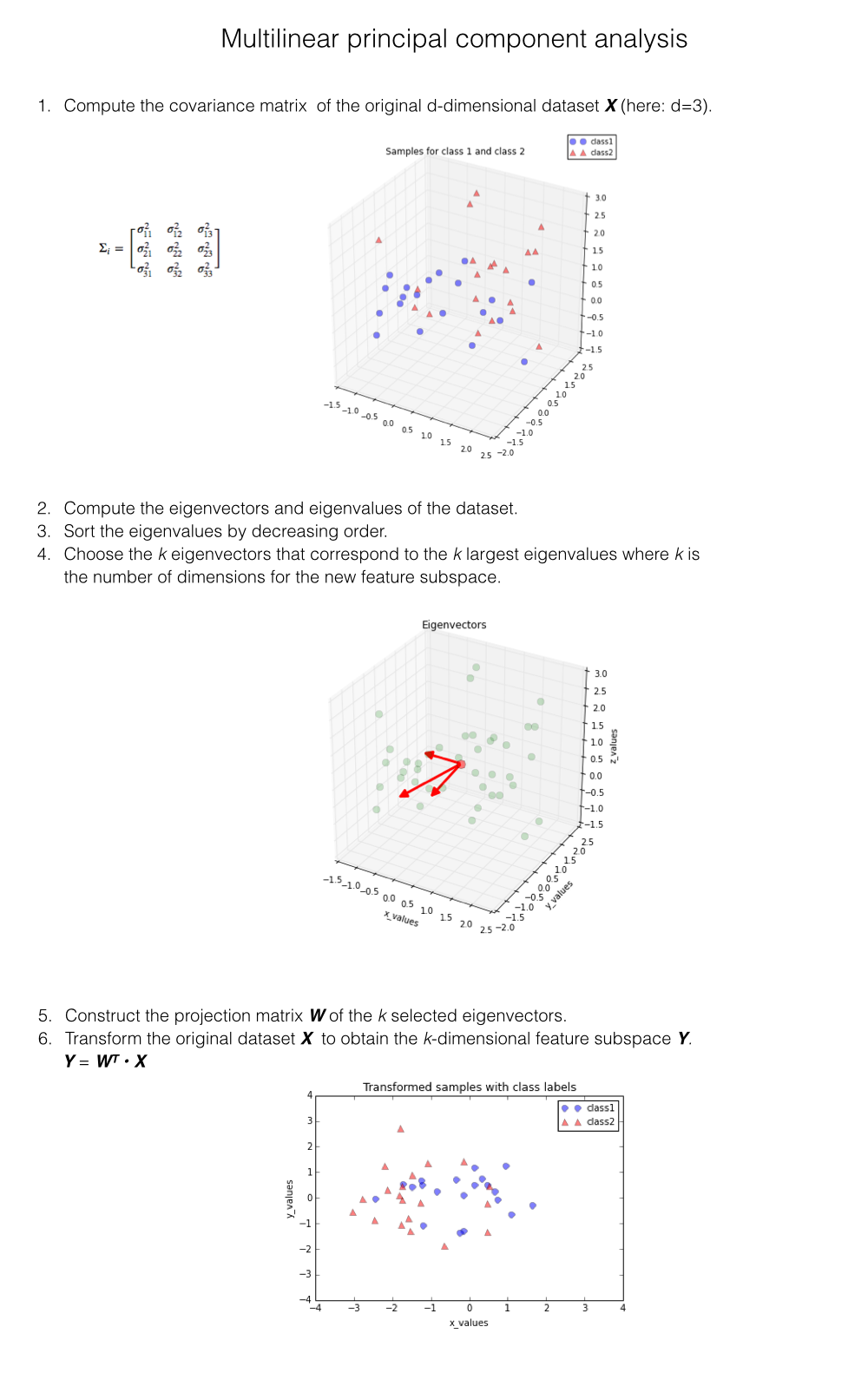
More details can be found in a previous article “Implementing a Principal Component Analysis (PCA) in Python step by step”.
Nonlinear dimensionality reduction
The “classic” PCA approach described above is a linear projection technique that works well if the data is linearly separable. However, in the case of linearly inseparable data, a nonlinear technique is required if the task is to reduce the dimensionality of a dataset.
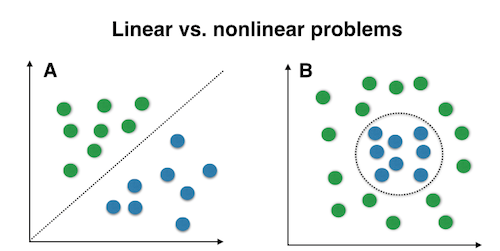
Kernel functions and the kernel trick
The basic idea to deal with linearly inseparable data is to project it onto a higher dimensional space where it becomes linearly separable. Let us call this nonlinear mapping function so that the mapping of a sample can be written as , which is called “kernel function.”
Now, the term “kernel” describes a function that calculates the dot product of the images of the samples under .
More details about the derivation of this equation are provided in this excellent review article by Quan Wang: Kernel Principal Component Analysis and its Applications in Face Recognition and Active Shape Models.[1]
In other words, the function maps the original d-dimensional features into a larger, k-dimensional feature space by creating nononlinear combinations of the original features. For example, if consists of 2 features:
Often, the mathematical definition of the RBF kernel is written and implemented as
\begin{equation} \kappa(\mathbf{x_i, x_j}) = exp\bigg(- \gamma \; \lVert\mathbf{x_i - x_j }\rVert^{2}_{2} \bigg)\end{equation}
where is a free parameter that is to be optimized.
Gaussian radial basis function (RBF) Kernel PCA
In the linear PCA approach, we are interested in the principal components that maximize the variance in the dataset. This is done by extracting the eigenvectors (principle components) that correspond to the largest eigenvalues based on the covariance matrix:
\begin{equation}\text{Cov} = \frac{1}{N} \sum_{i=1}^{N} \mathbf{x_i} \mathbf{x_i}^T \end{equation}
Bernhard Scholkopf (Kernel Principal Component Analysis [2]) generalized this approach for data that was mapped onto the higher dimensional space via a kernel function:
\begin{equation}\text{Cov} = \frac{1}{N} \sum_{i=1}^{N} \phi(\mathbf{x_i}) \phi(\mathbf{x_i})^T \end{equation}
However, in practice the the covariance matrix in the higher dimensional space is not calculated explicitly (kernel trick). Therefore, the implementation of RBF kernel PCA does not yield the principal component axes (in contrast to the standard PCA), but the obtained eigenvectors can be understood as projections of the data onto the principal components.
Implementing the RBF kernel PCA step-by-step
In order to implement the RBF kernel PCA we just need to consider the following two steps.
1. Computation of the kernel (similarity) matrix.
In this first step, we need to calculate
\begin{equation} \kappa(\mathbf{x_i, x_j}) = exp\bigg(- \gamma \; \lVert\mathbf{x_i - x_j }\rVert^{2}_{2} \bigg)\end{equation}
for every pair of points. E.g., if we have a dataset of 100 samples, this step would result in a symmetric 100x100 kernel matrix.
2. Eigendecomposition of the kernel matrix.
Since it is not guaranteed that the kernel matrix is centered, we can apply the following equation to do so:
\begin{equation} K’ = K - \mathbf{1_N} K - K \mathbf{1_N} + \mathbf{1_N} K \mathbf{1_N} \end{equation}
where is (like the kernel matrix) a matrix with all values equal to . [3]
Now, we have to obtain the eigenvectors of the centered kernel matrix that correspond to the largest eigenvalues. Those eigenvectors are the data points already projected onto the respective principal components.
Below, we implement those steps in Python to see how those computations work.
from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def stepwise_kpca(X, gamma, n_components):
"""
Implementation of a RBF kernel PCA.
Arguments:
X: A MxN dataset as NumPy array where the samples are stored as rows (M),
and the attributes defined as columns (N).
gamma: A free parameter (coefficient) for the RBF kernel.
n_components: The number of components to be returned.
"""
# Calculating the squared Euclidean distances for every pair of points
# in the MxN dimensional dataset.
sq_dists = pdist(X, 'sqeuclidean')
# Converting the pairwise distances into a symmetric MxM matrix.
mat_sq_dists = squareform(sq_dists)
# Computing the MxM kernel matrix.
K = exp(-gamma * mat_sq_dists)
# Centering the symmetric NxN kernel matrix.
N = K.shape[0]
one_n = np.ones((N,N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# Obtaining eigenvalues in descending order with corresponding
# eigenvectors from the symmetric matrix.
eigvals, eigvecs = eigh(K)
# Obtaining the i eigenvectors that corresponds to the i highest eigenvalues.
X_pc = np.column_stack((eigvecs[:,-i] for i in range(1,n_components+1)))
return X_pc
Examples of RBF Kernel PCA
In this section, we will apply the RBF kernel PCA to different nonlinear sample data in order to perform dimensionality reduction.
Half-moon shapes
We will start with a simple example of 2 half-moon shapes generated by the make_moons function from scikit-learn.
%matplotlib inline
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, random_state=123)
plt.figure(figsize=(8,6))
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', alpha=0.5)
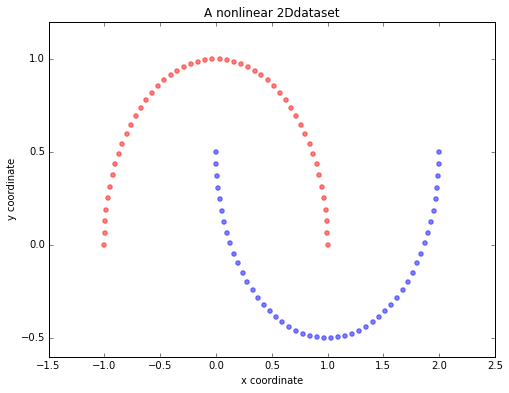
plt.title('A nonlinear 2Ddataset')
plt.ylabel('y coordinate')
plt.xlabel('x coordinate')
plt.show()
/Users/sebastian/miniconda3/envs/py34/lib/python3.4/site-packages/sklearn/datasets/samples_generator.py:612: DeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
y = np.hstack([np.zeros(n_samples_in, dtype=np.intp),
Linear PCA
Since the two half-moon shapes are linearly inseparable, we expect that the “classic” PCA will fail to give us a “good” representation of the data in 1D space. Here, we will use the PCA class that is implemented in scikit-learn to perform the dimensionality reduction.
from sklearn.decomposition import PCA
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
plt.figure(figsize=(8,6))
plt.scatter(X_spca[y==0, 0], X_spca[y==0, 1], color='red', alpha=0.5)
plt.scatter(X_spca[y==1, 0], X_spca[y==1, 1], color='blue', alpha=0.5)
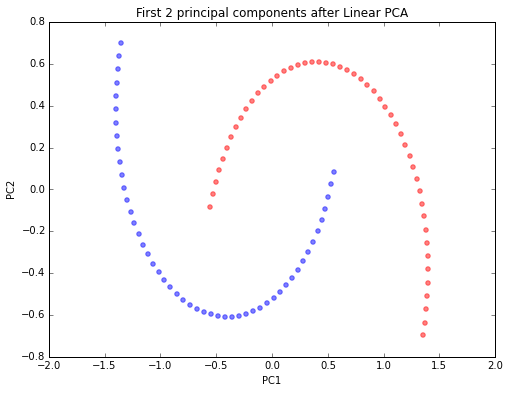
plt.title('First 2 principal components after Linear PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
import numpy as np
scikit_pca = PCA(n_components=1)
X_spca = scikit_pca.fit_transform(X)
plt.figure(figsize=(8,6))
plt.scatter(X_spca[y==0, 0], np.zeros((50,1)), color='red', alpha=0.5)
plt.scatter(X_spca[y==1, 0], np.zeros((50,1)), color='blue', alpha=0.5)
plt.title('First principal component after Linear PCA')
plt.xlabel('PC1')
plt.show()
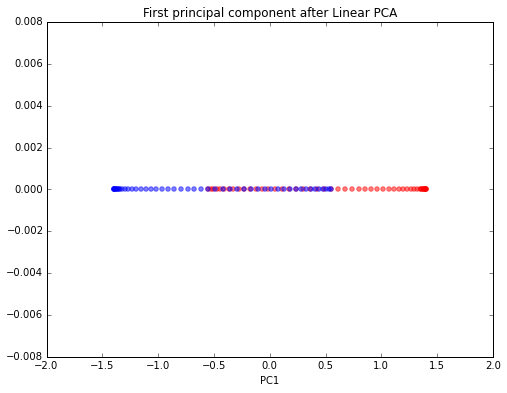
As we can see, the resulting principal components do not yield a subspace where the data is linearly separated well. Note that PCA is a unsupervised method and does not “consider” class labels in order to maximize the variance in contrast to Linear Discriminant Analysis. Here, the colors blue and red are just added for visualization purposes to indicate the degree of separation.
Gaussian RBF kernel PCA
Next, we will perform dimensionality reduction via RBF kernel PCA on our half-moon data. The choice of depends on the dataset and can be obtained via hyperparameter tuning techniques like Grid Search. Hyperparameter tuning is a broad topic itself, and here I will just use a -value that I found to produce “good” results.
X_pc = stepwise_kpca(X, gamma=15, n_components=2)
plt.figure(figsize=(8,6))
plt.scatter(X_pc[y==0, 0], X_pc[y==0, 1], color='red', alpha=0.5)
plt.scatter(X_pc[y==1, 0], X_pc[y==1, 1], color='blue', alpha=0.5)
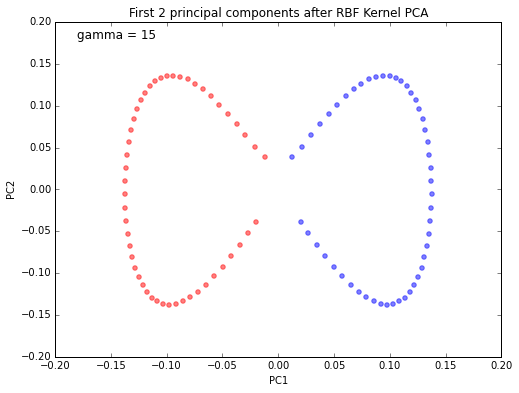
plt.title('First 2 principal components after RBF Kernel PCA')
plt.text(-0.18, 0.18, 'gamma = 15', fontsize=12)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
plt.figure(figsize=(8,6))
plt.scatter(X_pc[y==0, 0], np.zeros((50)), color='red', alpha=0.5)
plt.scatter(X_pc[y==1, 0], np.zeros((50)), color='blue', alpha=0.5)
plt.title('First principal component after RBF Kernel PCA')
plt.text(-0.17, 0.007, 'gamma = 15', fontsize=12)
plt.xlabel('PC1')
plt.show()
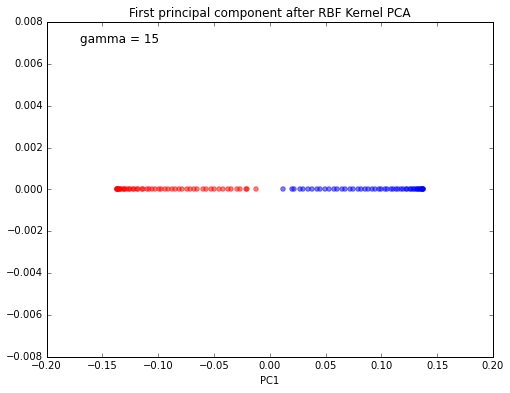
We can clearly see that the projection via RBF kernel PCA yielded a subspace where the classes are separated well. Such a subspace can then be used as input for linear classification models, such as Support Vector Machines or naive Bayes classifiers, which will be covered in future articles.
scikit RBF kernel PCA
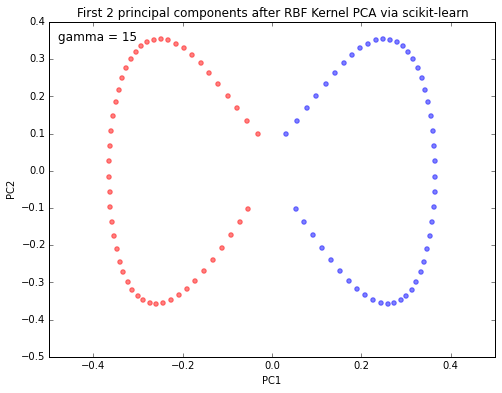
For our convenience, there is already an implementation of the KernelPCA in scikit-learn. Let us confirm that the results of our implementation is consistent with scikit-learn’s approach.
from sklearn.decomposition import KernelPCA
scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)
plt.figure(figsize=(8,6))
plt.scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1], color='red', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1], color='blue', alpha=0.5)
plt.text(-0.48, 0.35, 'gamma = 15', fontsize=12)
plt.title('First 2 principal components after RBF Kernel PCA via scikit-learn')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
scikit_kpca = KernelPCA(n_components=1, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)
plt.figure(figsize=(8,6))
plt.scatter(X_skernpca[y==0, 0], np.zeros((50,1)), color='red', alpha=0.5)
plt.scatter(X_skernpca[y==1, 0], np.zeros((50,1)), color='blue', alpha=0.5)
plt.text(-0.48, 0.007, 'gamma = 15', fontsize=12)
plt.title('First principal component after RBF Kernel PCA')
plt.xlabel('PC1')
plt.show()
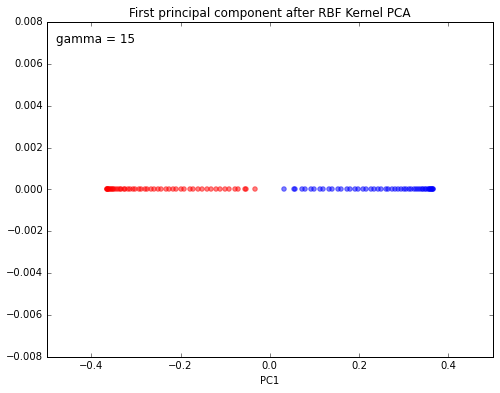
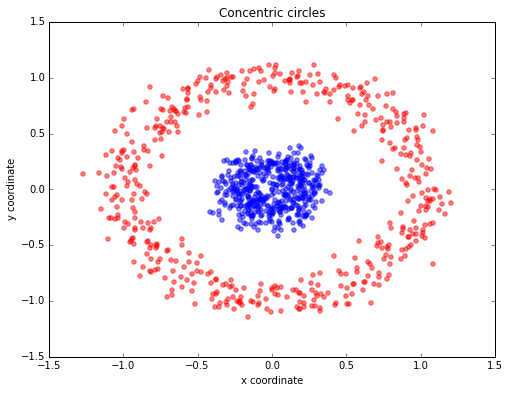
Concentric circles
For our next example, we will have a look at the classic case of 2 concentric circles with random noise produced by scikit-learn’s make_circles.
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)
plt.figure(figsize=(8,6))
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', alpha=0.5)
plt.title('Concentric circles')
plt.ylabel('y coordinate')
plt.xlabel('x coordinate')
plt.show()
Linear PCA
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
plt.figure(figsize=(8,6))
plt.scatter(X[y==0, 0], np.zeros((500,1))+0.1, color='red', alpha=0.5)
plt.scatter(X[y==1, 0], np.zeros((500,1))-0.1, color='blue', alpha=0.5)
plt.ylim([-15,15])
plt.text(-0.125, 12.5, 'gamma = 15', fontsize=12)
plt.title('First principal component after Linear PCA')
plt.xlabel('PC1')
plt.show()
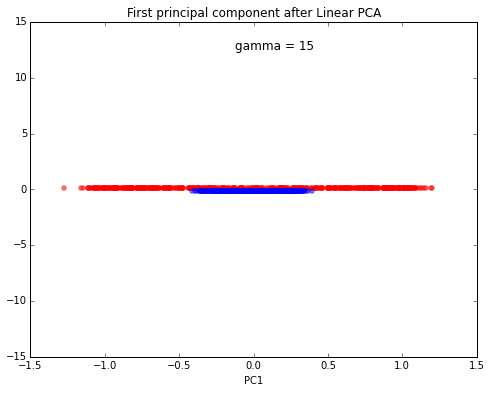
Again, the results obtained via the linear PCA approach does not produce a subspace where the 2 classes are linearly well separated.
Gaussian RBF kernel PCA
X_pc = stepwise_kpca(X, gamma=15, n_components=1)
plt.figure(figsize=(8,6))
plt.scatter(X_pc[y==0, 0], np.zeros((500,1)), color='red', alpha=0.5)
plt.scatter(X_pc[y==1, 0], np.zeros((500,1)), color='blue', alpha=0.5)
plt.text(-0.05, 0.007, 'gamma = 15', fontsize=12)
plt.title('First principal component after RBF Kernel PCA')
plt.xlabel('PC1')
plt.show()
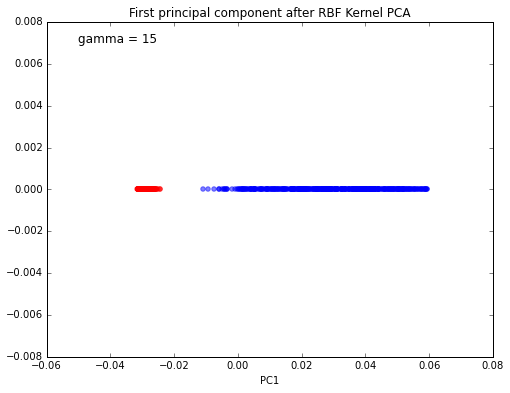
And again, this 1-dimensional subspace obtained via Gaussian RBF kernel PCA looks much better in terms of linear class separation.
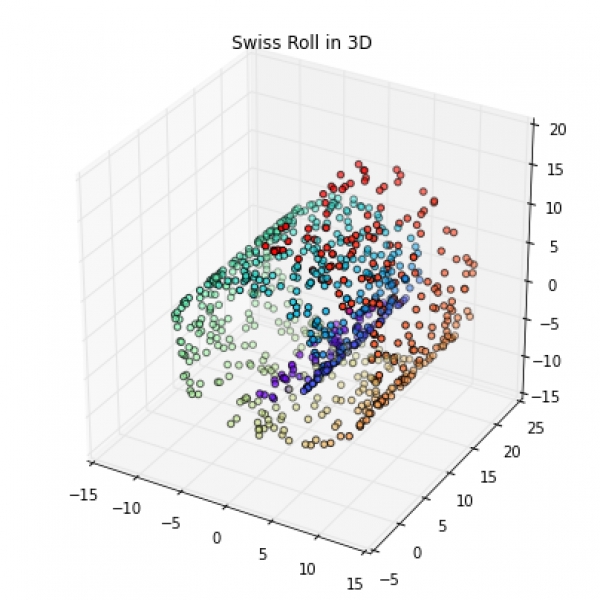
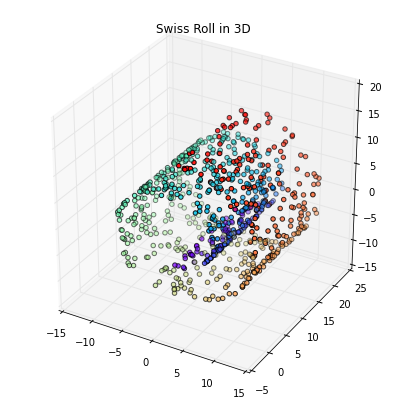
Swiss roll
Unrolling the famous Swiss roll is a more challenging task than the examples we have seen above. We will use the make_swiss_roll to create 3-dimensional Swiss roll and start with the linear PCA to project the dataset onto a 2D and 1D feature subspace.
from sklearn.datasets.samples_generator import make_swiss_roll
from mpl_toolkits.mplot3d import Axes3D
X, color = make_swiss_roll(n_samples=800, random_state=123)
fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.rainbow)
plt.title('Swiss Roll in 3D')
plt.show()
Linear PCA
from sklearn.decomposition import PCA
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
plt.figure(figsize=(8,6))
plt.scatter(X_spca[:, 0], X_spca[:, 1], c=color, cmap=plt.cm.rainbow)
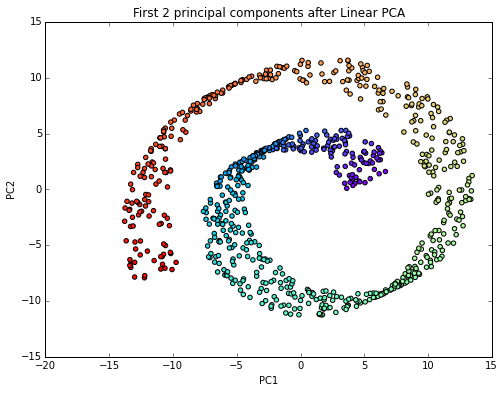
plt.title('First 2 principal components after Linear PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
scikit_pca = PCA(n_components=1)
X_spca = scikit_pca.fit_transform(X)
plt.figure(figsize=(8,6))
plt.scatter(X_spca, np.zeros((800,1)), c=color, cmap=plt.cm.rainbow)
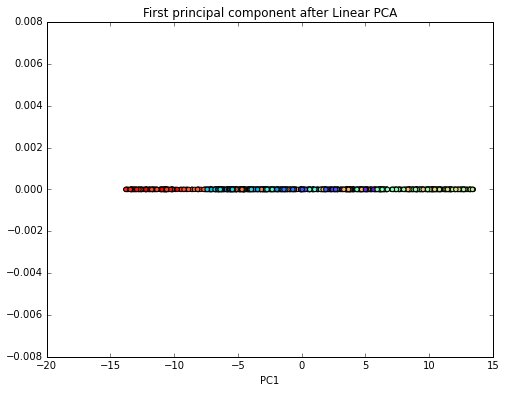
plt.title('First principal component after Linear PCA')
plt.xlabel('PC1')
plt.show()
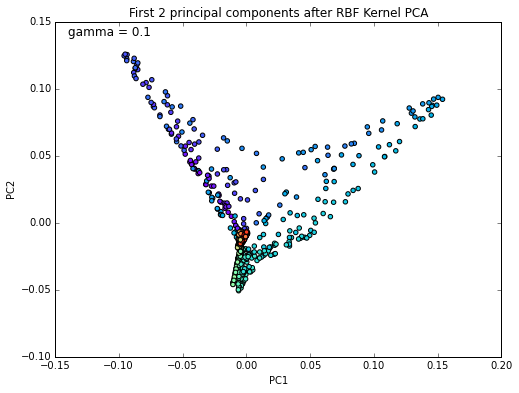
Gaussian RBF kernel PCA
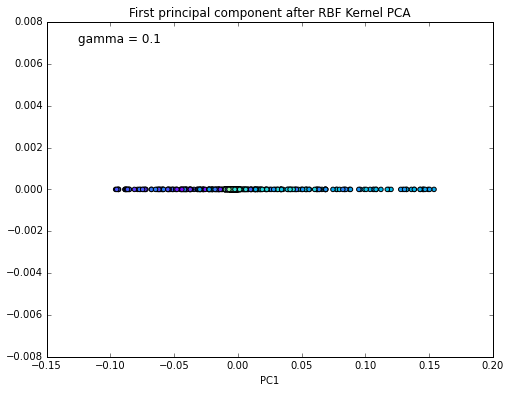
I haven’t found a good parameter for the Gaussian RBF kernel for good linear separation of this dataset. The best result I obtained is shown in the following figures.
X_pc = stepwise_kpca(X, gamma=0.1, n_components=2)
plt.figure(figsize=(8,6))
plt.scatter(X_pc[:, 0], X_pc[:, 1], c=color, cmap=plt.cm.rainbow)
plt.title('First 2 principal components after RBF Kernel PCA')
plt.text(-0.14, 0.14, 'gamma = 0.1', fontsize=12)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
plt.figure(figsize=(8,6))
plt.scatter(X_pc[:,0], np.zeros((800,1)), c=color, cmap=plt.cm.rainbow)
plt.text(-0.125, 0.007, 'gamma = 0.1', fontsize=12)
plt.title('First principal component after RBF Kernel PCA')
plt.xlabel('PC1')
plt.show()
Locally-Linear Embedding (LLE)
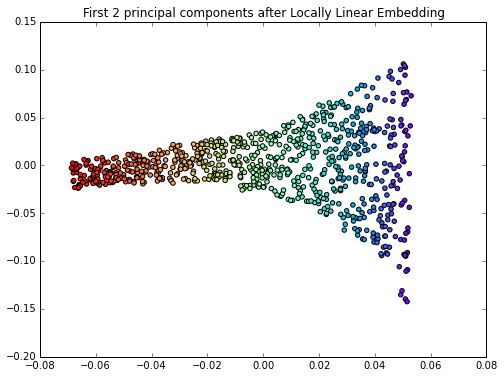
In 2000, Sam T. Roweis and Lawrence K. Saul (Nonlinear dimensionality reduction by locally linear embedding [4]) introduced an unsupervised learning algorithm called locally linear embedding (LLE) that is better suited to identify patterns in the high-dimensional feature space and solves our problem of nonlinear dimensionality reduction for the Swiss roll.
Here, we will use the locally_linear_embedding class from scikit-learn to “unroll” the Swiss roll.
from sklearn.manifold import locally_linear_embedding
X_lle, err = locally_linear_embedding(X, n_neighbors=12, n_components=2)
plt.figure(figsize=(8,6))
plt.scatter(X_lle[:, 0], X_lle[:, 1], c=color, cmap=plt.cm.rainbow)
plt.title('First 2 principal components after Locally Linear Embedding')
plt.show()
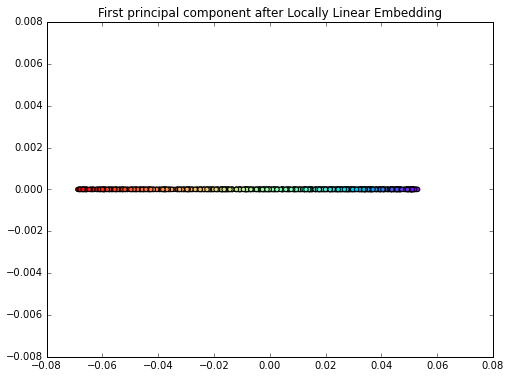
from sklearn.manifold import locally_linear_embedding
X_lle, err = locally_linear_embedding(X, n_neighbors=12, n_components=1)
plt.figure(figsize=(8,6))
plt.scatter(X_lle, np.zeros((800,1)), c=color, cmap=plt.cm.rainbow)
plt.title('First principal component after Locally Linear Embedding')
plt.show()
Appendix A: Projecting new data
So far, so good, in the sections above, we have been projecting an dataset onto a new feature subspace. However, in a real application, we are usually interested in mapping new data points onto the same new feature subspace (e.g., if are working with a training and a test dataset in pattern classification tasks).
Remember, when we computed the eigenvectors \( \mathbf{\alpha} \) of the centered kernel matrix, those values were actually already the projected datapoints onto the principal component axis \( \mathbf{g} \).
If we want to project a new data point \( \mathbf{x} \) onto this principal component axis, we’d need to compute \(\phi(\mathbf{x})^T \mathbf{g} \).
Fortunately, also here, we don’t have to compute \(\phi(\mathbf{x})^T \mathbf{g} \) explicitely but use the kernel trick to calculate the RBF kernel between the new data point and every data point \( j \) in the training dataset:
and the eigenvectors \( \alpha \) and eigenvalues \( \lambda \) of the Kernel matrix \(\mathbf{K}\) satisfy the equation \(\mathbf{K} \alpha = \lambda \alpha \), we just need to normalize the eigenvector by the corresponding eigenvalue.
First, let us modify our original implementation by returning the corresponding to return also the eigenvalues of the kernel matrix.
from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def stepwise_kpca(X, gamma, n_components):
"""
Implementation of a RBF kernel PCA.
Arguments:
X: A MxN dataset as NumPy array where the samples are stored as rows (M),
and the attributes defined as columns (N).
gamma: A free parameter (coefficient) for the RBF kernel.
n_components: The number of components to be returned.
Returns the k eigenvectors (alphas) that correspond to the k largest
eigenvalues (lambdas).
"""
# Calculating the squared Euclidean distances for every pair of points
# in the MxN dimensional dataset.
sq_dists = pdist(X, 'sqeuclidean')
# Converting the pairwise distances into a symmetric MxM matrix.
mat_sq_dists = squareform(sq_dists)
# Computing the MxM kernel matrix.
K = exp(-gamma * mat_sq_dists)
# Centering the symmetric NxN kernel matrix.
N = K.shape[0]
one_n = np.ones((N,N)) / N
K_norm = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# Obtaining eigenvalues in descending order with corresponding
# eigenvectors from the symmetric matrix.
eigvals, eigvecs = eigh(K_norm)
# Obtaining the i eigenvectors (alphas) that corresponds to the i highest eigenvalues (lambdas).
alphas = np.column_stack((eigvecs[:,-i] for i in range(1,n_components+1)))
lambdas = [eigvals[-i] for i in range(1,n_components+1)]
return alphas, lambdas
Now, let’s make a new half-moon dataset and project it onto a 1-dimensonal subspace using the RBF kernel PCA:
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, random_state=123)
alphas, lambdas = stepwise_kpca(X, gamma=15, n_components=1)
/Users/sebastian/miniconda3/envs/py34/lib/python3.4/site-packages/sklearn/datasets/samples_generator.py:612: DeprecationWarning: using a non-integer number instead of an integer will result in an error in the future
y = np.hstack([np.zeros(n_samples_in, dtype=np.intp),
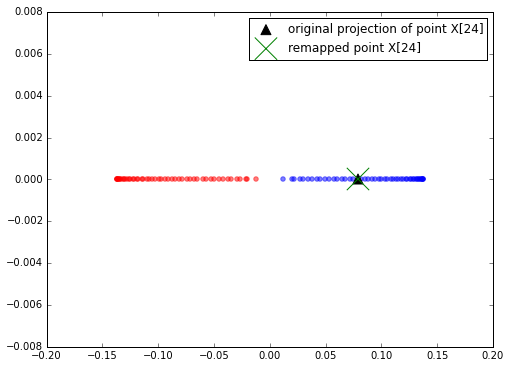
To confirm that our approach produces the correct results, let’s pretend that the 24th point from the half-moon dataset is a new data point \( \mathbf{x} \), and we want to project it onto this new subspace.
x_new = X[25]
X_proj = alphas[25] # original projection
x_new
array([ 1.8713187 , 0.00928245])
X_proj
array([ 0.07877284])
def project_x(x_new, X, gamma, alphas, lambdas):
pair_dist = np.array([np.sum((x_new-row)**2) for row in X])
k = np.exp(-gamma * pair_dist)
return k.dot(alphas / lambdas)
# projection of the "new" datapoint
x_reproj = project_x(x_new, X, gamma=15, alphas=alphas, lambdas=lambdas)
x_reproj
array([ 0.07877284])
%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
plt.scatter(alphas[y==0, 0], np.zeros((50)), color='red', alpha=0.5)
plt.scatter(alphas[y==1, 0], np.zeros((50)), color='blue', alpha=0.5)
plt.scatter(X_proj, 0, color='black', label='original projection of point X[24]', marker='^', s=100)
plt.scatter(x_reproj, 0, color='green', label='remapped point X[24]', marker='x', s=500)
plt.legend(scatterpoints=1)
plt.show()
References
[1] Q. Wang. Kernel principal component analysis and its applications in face recognition and active shape models. CoRR, abs/1207.3538, 2012. [2] B. Scholkopf, A. Smola, and K.-R. Muller. Kernel principal component analysis. pages 583–588, 1997. [3] B. Scholkopf, A. Smola, and K.-R. Muller. Nonlinear component analysis as a kernel eigenvalue problem. Neural computation, 10(5):1299–1319, 1998. [4] S. T. Roweis and L. K. Saul. Nonlinear dimensionality reduction by locally linear embedding. Science, 290(5500):2323–2326, 2000.source: http://sebastianraschka.com/Articles/2014_kernel_pca.html