Blog
Understanding Bayesian A/B testing (using baseball statistics)
Written by Sayed Jamal MirkamaliWell, Mike Piazza has a slightly higher career batting average (2127 hits / 6911 at-bats = 0.308) than Hank Aaron (3771 hits / 12364 at-bats = 0.305). But can we say with confidence that his skill is actually higher, or is it possible he just got lucky a bit more often?
In this series of posts about an empirical Bayesian approach to batting statistics, we’ve been estimating batting averages by modeling them as a binomial distribution with a beta prior. But we’ve been looking at a single batter at a time. What if we want to compare two batters, give a probability that one is better than the other, and estimate by how much?
This is a topic rather relevant to my own work and to the data science field, because understanding the difference between two proportions is important in A/B testing. One of the most common examples of A/B testing is comparing clickthrough rates (“out of X impressions, there have been Y clicks”)- which on the surface is similar to our batting average estimation problem (“out of X at-bats, there have been Y hits””).1
Here, we’re going to look at an empirical Bayesian approach to comparing two batters.2 We’ll define the problem in terms of the difference between each batter’s posterior distribution, and look at four mathematical and computational strategies we can use to resolve this question. While we’re focusing on baseball here, remember that similar strategies apply to A/B testing, and indeed to many Bayesian models.
Python - Kernel tricks and nonlinear dimensionality reduction via RBF kernel PCA
Written by Sayed Jamal Mirkamali
Most machine learning algorithms have been developed and statistically validated for linearly separable data. Popular examples are linear classifiers like Support Vector Machines (SVMs) or the (standard) Principal Component Analysis (PCA) for dimensionality reduction. However, most real world data requires nonlinear methods in order to perform tasks that involve the analysis and discovery of patterns successfully.
The focus of this article is to briefly introduce the idea of kernel methods and to implement a Gaussian radius basis function (RBF) kernel that is used to perform nonlinear dimensionality reduction via BF kernel principal component analysis (kPCA).
Machine Learning is dead - Long live machine learning!
Written by Sayed Jamal Mirkamali
You may be thinking that this title makes no sense at all. ML, AI, ANN and Deep learning have made it into the everyday lexicon and here I am, proclaiming that ML is dead. Well, here is what I mean…
The open sourcing of entire ML frameworks marks the end of a phase of rapid development of tools, and thus marks the death of ML as we have known it so far. The next phase will be marked with ubiquitous application of these tools into software applications. And that is how ML will live forever, because it will seamlessly and inextricably integrate into our lives.
Rootograms, A new way to assess count models
Written by Sayed Jamal Mirkamali
Assessing the fit of a count regression model is not necessarily a straightforward enterprise; often we just look at residuals, which invariably contain patterns of some form due to the discrete nature of the observations, or we plot observed versus fitted values as a scatter plot. Recently, while perusing the latest statistics offerings on ArXiv I came across Kleiber and Zeileis (2016) who propose the rootogram as an improved approach to the assessment of fit of a count regression model. The paper is illustrated using R and the authors’ countreg package (currently on R-Forge only). Here, I thought I’d take a quick look at the rootogram with some simulated species abundance data.
The concept is certainly compelling. Having a machine capable of reacting to real-world visual, auditory or other type of data and then responding, in an intelligent way, has been the stuff of science fiction until very recently. We are now on the verge of this new reality with little general understanding of what it is that artificial intelligence, convolutional neural networks, and deep learning can (and can’t) do, nor what it takes to make them work. At the simplest level, much of the current efforts around deep learning involve very rapid recognition and classification of objects—whether visual, audible, or some other form of digital data. Using cameras, microphones and other types of sensors, data is input into a system that contains a multi-level set of filters that provide increasingly detailed levels of differentiation. Think of it like the animal or plant classification charts from your grammar school days: Kingdom, Phylum, Class, Order, Family, Genus, Species.
Search
Archive
Latest Posts
Latest Comments
K2 Content
-
A synergetic R-Shiny portal for modeling and tracking of COVID-19 data
Written by S. Morteza NajibiWritten on Friday, 08 January 2021 07:03 in SDAT News Read 4519 times Read more...
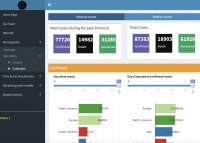
Dr. Mahdi Salehi, an associate member of SDAT and assistant professor of statistics at the University of Neyshabur, introduced a useful online interactive dashboard that visualize and follows confirmed cases of COVID-19 in real-time. The dashboard was publicly made available on 6 April 2020 to illustrate the counts of confirmed cases, deaths, and recoveries of COVID-19 at the level of country or continent. This dashboard is intended as a user-friendly dashboard for researchers as well as the general public to track the COVID-19 pandemic, and is generated from trusted data sources and built-in open-source R software (Shiny in particular); ensuring a high sense of transparency and reproducibility.
Access the shiny dashboard: https://mahdisalehi.shinyapps.io/Covid19Dashboard/
-
First Event on Play with Real Data
Written by S. Morteza NajibiWritten on Wednesday, 23 December 2020 13:45 in SDAT News Read 4782 times Read more...
Scientific Data Analysis Team (SDAT) intends to organize the first event on the value of data to provide data holders and data analyzers with an opportunity to extract maximum value from their data. This event is organized by International Statistical Institute (ISI) and SDAT hosted at the Bu-Ali Sina University, Hamedan, Iran.
Organizers and the data providers will provide more information about the goals of the initial ideas, team arrangement, competition processes, and the benefits of attending this event on a webinar hosted at the ISI Gotowebianr system. Everyone invites to participate in this webinar for free, but it is needed to register at the webinar system by 30 December 2020.
Event Time: 31 December 2020 - 13:30-16:30 Central European Time (CET)
Register for the webinar: https://register.gotowebinar.com/register/8913834636664974352
More details about this event: http://sdat.ir/en/playdata
Aims and outputs:
• Playing with real data by explorative and predictive data analysis techniques
• A platform between a limited number of data providers and hundreds to thousands of data scientist Teams
• Improving creativity and scientific reasoning of data scientist and statisticians
• Finding the possible “bugs” with the current data analysis methods and new developments
• Learn different views about a dataset.AWARD-WINNING:
The best-report awards consist of a cash prize:
$400 for first place,
$200 for second place, and
$100 for third place.Important Dates:
Event Webinar: 31 December 2020 - 13:30-16:30 Central European Time (CET).
Team Arrangement: 01 Jan. 2021 - 07 Jan. 2021
Competition: 10 Jan. 2021 - 15 Jan. 2021
First Assessment Result: 25 Jan. 2021
Selected Teams Webinar: 30 Jan. 2021
Award Ceremony: 31 Jan. 2021Please share this event with your colleagues, students, and data analyzers.
-
Development of Neuroimaging Symposium and Advanced fMRI Data Analysis
Written by S. Morteza NajibiWritten on Sunday, 21 April 2019 12:18 in SDAT News Read 4914 times Read more...
The Developement of Structural and Functional Neuroimaging Symposium hold at the School of Sciences, Shiraz University in April 17 2019. The Advanced fMRI Data Analysis Workshop also held in April 18-19 2019. For more information please visit: http://sdat.ir/dns98
-
Releasing Rfssa Package by SDAT Members at CRAN
Written by S. Morteza NajibiWritten on Sunday, 03 March 2019 21:03 in SDAT News Read 3513 times
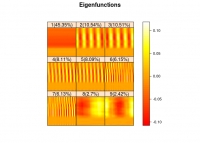
The Rfssa package is available at CRAN. Dr. Hossein Haghbin and Dr. Seyed Morteza Najibi (SDAT Members) have published this package to provide the collections of necessary functions to implement Functional Singular Spectrum Analysis (FSSA) for analysing Functional Time Series (FTS). FSSA is a novel non-parametric method to perform decomposition and reconstruction of FTS. For more information please visit github homepage of package.
-
Data Science Symposium
Written by S. Morteza NajibiWritten on Friday, 01 February 2019 00:13 in SDAT News Read 5009 times Read more...
Symposium of Data Science Developement and its job opportunities hold at the Faculty of Science, Shiraz University in Feb 20 2019. For more information please visit: http://sdat.ir/dss97
Tags
About Us
SDAT is an abbreviation for Scientific Data Analysis Team. It consists of groups who are specialists in various fields of data sciences including Statistical Analytics, Business Analytics, Big Data Analytics and Health Analytics.
Get In Touch
Address: No.15 13th West Street, North Sarrafan, Apt. No. 1 Saadat Abad- Tehran
Phone: +98-910-199-2800
Email: info@sdat.ir